Parameters

Defining default parameters

When you create a module using Starsim, you have the opportunity to define the default format for parameters. Let’s look at an example from the SIR disease model:

import starsim as ss

class MySIR(ss.SIR):
    def __init__(self, **kwargs):
        super().__init__()
        self.define_pars(
            beta = ss.peryear(0.1),
            init_prev = ss.bernoulli(p=0.01),
            dur_inf = ss.lognorm_ex(mean=ss.years(6)),
            p_death = ss.bernoulli(p=0.01),
        )
        self.update_pars(**kwargs)

        self.define_states(
            ss.BoolState('susceptible', default=True, label='Susceptible'),
            ss.BoolState('infected', label='Infectious'),
            ss.BoolState('recovered', label='Recovered'),
            ss.FloatArr('ti_infected', label='Time of infection'),
            ss.FloatArr('ti_recovered', label='Time of recovery'),
            ss.FloatArr('ti_dead', label='Time of death'),
            ss.FloatArr('rel_sus', default=1.0, label='Relative susceptibility'),
            ss.FloatArr('rel_trans', default=1.0, label='Relative transmission'),
            reset = True, # Do not use any existing states
        )
        return

The point of self.define_pars() is to set the ground truth for the format that the parameters should take. When users enter their own parameters for defining an instance of this module, the parameter values they enter will be processed within self.update_pars() and will be checked for consistency with the format provided in the original parameters (define_pars). For example, the parameter p_death in the SIR example above is specified initially as a Bernoulli distribution. It would be perfectly legitimate to create an instance of the SIR model using any of the following formats:

sir1 = MySIR(p_death=0.02)
sir2 = MySIR(p_death=ss.bernoulli(p=0.2))

However, it would NOT be ok to create an SIR model with e.g. MySIR(p_death=ss.lognorm_ex(4)), because if a distribution is defined as a Bernoulli in the default_pars, it can’t be changed. This is only the case for Bernoulli distributions; other distributions can be changed, e.g. MySIR(dur_inf=ss.normal(4)) would be okay. This is because Bernoulli distributions have different methods than other distributions, e.g. a filter() method that returns True for agents which pass the filter.

Using callable parameters

One of the most flexible aspects of how Starsim’s distributions are defined is that they can take callable functions as parameter values. For example, in reality the duration of infection of a disease might vary by age. We could model this as follows:

import sciris as sc
import matplotlib.pyplot as plt
import starsim as ss

# Create and run the simulation
sir = ss.SIR(dur_inf=ss.normal(loc=ss.years(10)))  # Define an SIR model with a default duration of 10 days
sir.pars.dur_inf.set(loc = lambda self, sim, uids: sim.people.age[uids] / 10)  # Change the mean duration so it scales with age
sim = ss.Sim(n_agents=20e3, dur=10, diseases=sir, networks='random')
sim.run()
sim.plot()

# Show the age distribution of infections
ages = sim.people.age[:]
infected_ages = ages[sim.diseases.sir.infected]

fig = plt.figure()

plt.subplot(2,1,1)
plt.hist(ages, bins=range(0,100,5))
plt.title('Simulation age distribution')
plt.xlabel('Age')
plt.ylabel('Number of people')

plt.subplot(2,1,2)
plt.hist(infected_ages, bins=range(0,100,5))
plt.title('Infection age distribution')
plt.xlabel('Age')
plt.ylabel('Number of people')

sc.figlayout()
plt.show()

Initializing sim with 20000 agents
  Running 2000.01.01 ( 0/11) (0.00 s)  •——————————————————— 9%
  Running 2010.01.01 (10/11) (0.20 s)  •••••••••••••••••••• 100%

Figure(768x576)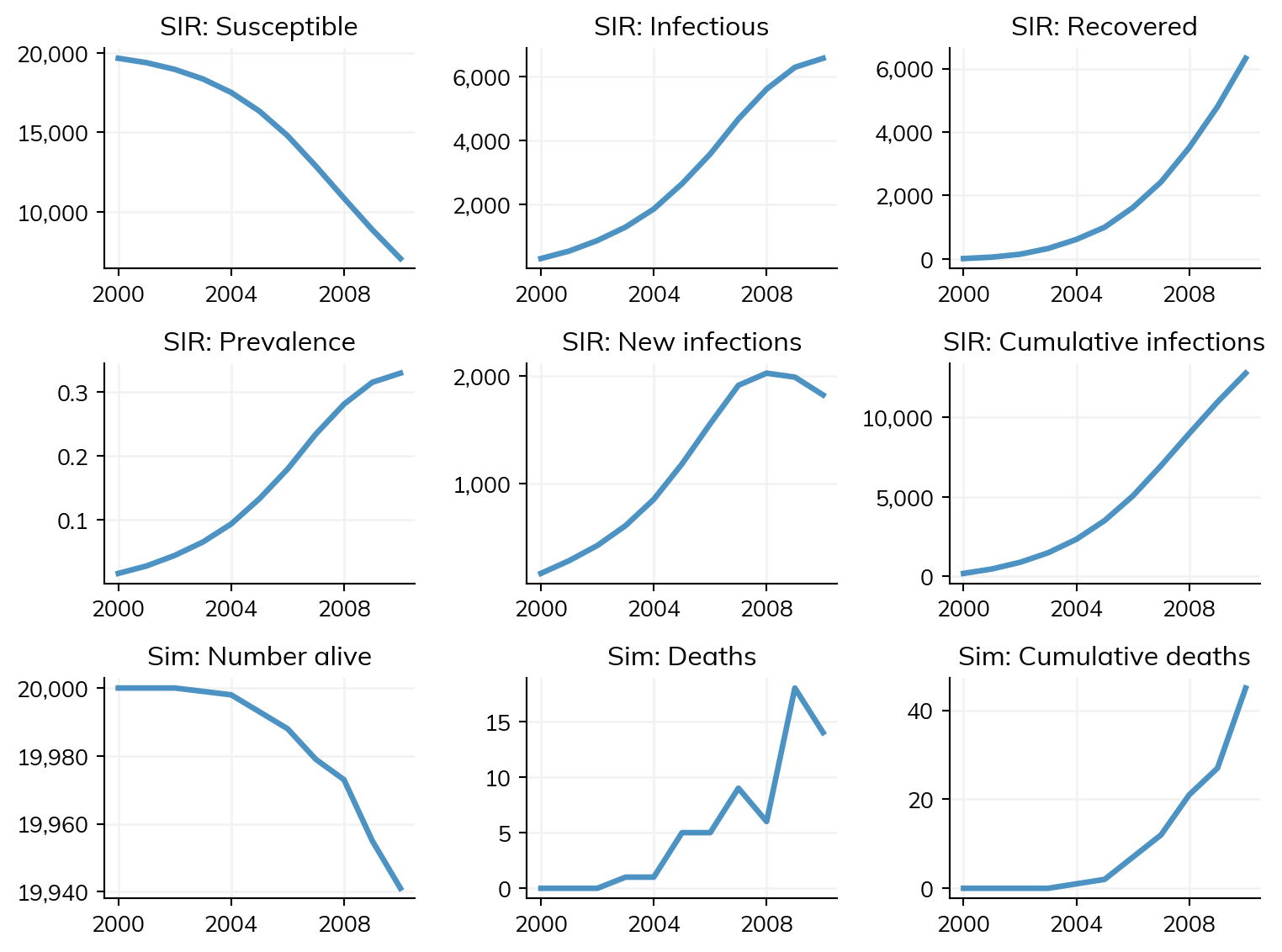

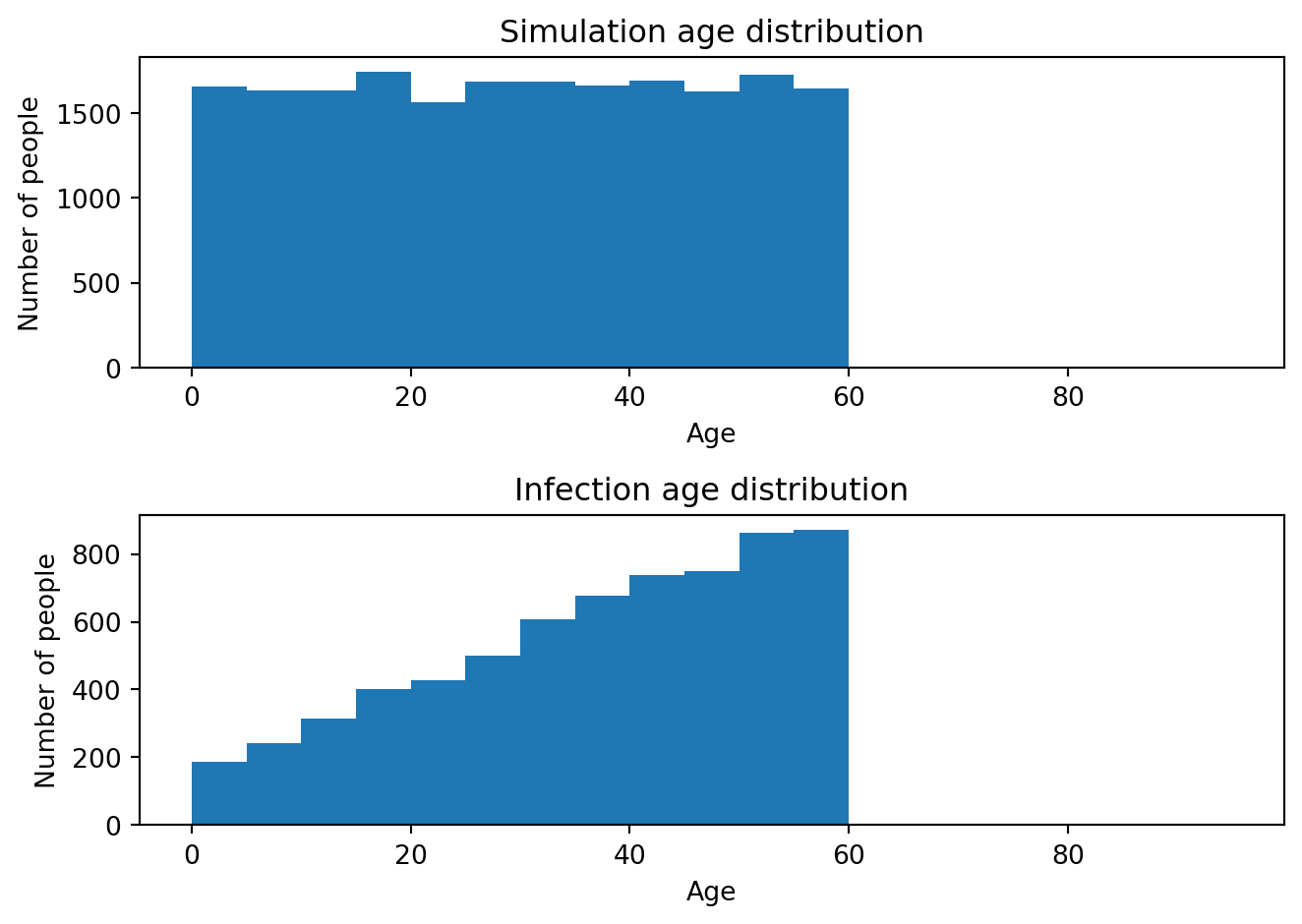
Using similar logic, any other parameter could be set to depend on anything that the sim is aware of, including time or agent properties like age, sex, or health attributes.